1. Welcome to our comprehensive guide on "System of Particles and Rotational Motion" Multiple-Choice Questions (MCQs) tailored specifically for the HTET 2023 exam. If you're gearing up for this challenging test, you've come to the right place. In this blog, we'll provide you with a valuable resource to enhance your understanding of the core concepts, test your knowledge, and offer expert tips to help you excel in this crucial section of the HTET. Let's dive in!
1.When an external torque is applied to a system of particles, what is the effect on its angular momentum?
A) Angular momentum remains constant
B) Angular momentum increases
C) Angular momentum decreases
D) Angular momentum changes direction
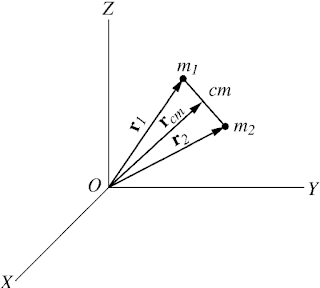
2. In a system of particles, what is the center of mass?
A) The point where all particles are located
B) The point where the total mass is concentrated
C) The point where the angular velocity is maximum
D) The point where the angular momentum is conserved
3. Which of the following is a rotational analog of Newton's second law (F = ma) for linear motion?
A) Torque = Moment of Inertia × Angular Acceleration
B) Force = Mass × Acceleration
C) Momentum = Mass × Velocity
D) Work = Force × Displacement
4. If the net external torque acting on a system of particles is zero, what can be said about its angular momentum?
A) Angular momentum is constant
B) Angular momentum decreases
C) Angular momentum increases
D) Angular momentum reverses direction
5. Which of the following is an example of an internal force in a system of particles?
A) Gravity acting on a falling object
B) Tension in a rope pulling an object
C) Friction between a wheel and the ground
D) The force exerted by one part of the system on another part
6. When a figure skater pulls in their arms during a spin, what happens to their angular velocity?
A) Angular velocity decreases
B) Angular velocity remains the same
C) Angular velocity increases
D) Angular velocity reverses direction
7. What is the moment of inertia of an object?
A) The force required to move the object linearly
B) The measure of an object's rotational inertia
C) The angular acceleration of the object
D) The torque applied to the object
8. Two identical disks are rotating about their central axes. Disk A has a greater rotational speed than Disk B. Which one has the greater kinetic energy?
A) Disk A
B) Disk B
C) They have the same kinetic energy
D) It depends on the mass of the disks
9. Which of the following quantities is always conserved in the absence of external torques in a closed system?
A) Angular momentum
B) Linear momentum
C) Kinetic energy
D) Potential energy
10. If a force is applied to the edge of a door perpendicular to its plane, causing it to rotate about its hinges, what is the pivot point called?
A) Axis of rotation
B) Center of mass
C) Torque point
D) Fulcrum
11. In a system of particles, if the net external torque acting on it is zero and the initial angular momentum is not zero, what can be concluded about the system's angular momentum?
A) It remains constant
B) It increases
C) It decreases
D) It reverses direction
12. Which of the following quantities depends on both the mass of an object and its distribution of mass around an axis of rotation?
A) Angular velocity
B) Angular momentum
C) Moment of inertia
D) Torque
13. When a diver tucks into a somersault during a dive, what happens to their angular momentum?
A) It increases
B) It decreases
C) It remains the same
D) It becomes zero
14. What is the term for the point in a rotating system where the entire mass can be considered concentrated for the purpose of calculating angular motion?
A) Center of gravity
B) Axis of rotation
C) Center of mass
D) Moment of inertia
15. If two objects have the same moment of inertia but different angular velocities, which one has the greater angular momentum?
A) The one with higher angular velocity
B) The one with lower angular velocity
C) Both have the same angular momentum
D) It depends on their mass
16. In a system of particles, what happens to the total angular momentum when particles move closer to the axis of rotation?
A) Total angular momentum increases
B) Total angular momentum decreases
C) Total angular momentum remains constant
D) Total angular momentum becomes zero
17. Which law of motion can be applied to rotational motion to relate the net external torque to the change in angular momentum?
A) Newton's First Law
B) Newton's Second Law
C) Newton's Third Law
D) Law of Conservation of Angular Momentum
18. When a figure skater with arms extended spins, and then pulls their arms in close to their body while continuing to spin, what happens to their angular velocity?
A) Angular velocity increases
B) Angular velocity decreases
C) Angular velocity remains the same
D) Angular velocity reverses direction
19. What is the name for the rotational analog of mass, which quantifies an object's resistance to changes in its angular motion?
A) Moment of inertia
B) Angular velocity
C) Angular acceleration
D) Torque
20. In a closed system of particles with no external torques acting on it, what happens to the total angular momentum?
A) It decreases
B) It remains the same
C) It increases
D) It becomes zero
21. When a rotating object experiences an external torque, what happens to its angular momentum?
A) Angular momentum remains constant
B) Angular momentum increases
C) Angular momentum decreases
D) Angular momentum changes direction
22. In a system of particles, what is the relationship between the moment of inertia and the distribution of mass?
A) The moment of inertia depends only on the total mass.
B) The moment of inertia depends only on the shape of the objects.
C) The moment of inertia depends on both the total mass and the distribution of mass.
D) The moment of inertia is not related to mass.
23. Which of the following equations represents the rotational analog of Newton's second law (F = ma) for linear motion?
A) τ = Iα (Torque = Moment of Inertia × Angular Acceleration)
B) F = ma (Force = Mass × Acceleration)
C) p = mv (Momentum = Mass × Velocity)
D) W = Fd (Work = Force × Displacement)
24. If a system of particles is rotating with a constant angular velocity, what can be concluded about the net external torque acting on it?
A) The net external torque is zero.
B) The net external torque is nonzero.
C) The net external torque changes direction.
D) The net external torque is undefined.
25. What is the condition for a system of particles to be in rotational equilibrium?
A) The net external torque must be nonzero.
B) The total angular momentum must be zero.
C) The sum of the external torques must be zero.
D) The moment of inertia must be infinite.
26. When a diver in a tuck position spins in the air, and then extends their body to slow down the rotation, what happens to their moment of inertia?
A) Moment of inertia decreases
B) Moment of inertia increases
C) Moment of inertia remains the same
D) Moment of inertia reverses direction
27. What is the point in a rotating system where the net external torque causes no change in the angular momentum called?
A) Axis of rotation
B) Center of mass
C) Torque point
D) Equilibrium point
28. Which of the following is a rotational analog of kinetic energy in linear motion?
A) Angular momentum
B) Moment of inertia
C) Angular velocity
D) Rotational kinetic energy
29. When a torque is applied to a rotating object in a direction opposite to its angular velocity, what happens to the object's rotation?
A) Angular velocity increases
B) Angular velocity remains the same
C) Angular velocity decreases
D) Angular velocity becomes zero
30. Which law of motion states that for every action, there is an equal and opposite reaction, and how does it relate to rotational motion?
A) Newton's First Law; it describes rotational equilibrium.
B) Newton's Second Law; it relates torque to angular acceleration.
C) Newton's Third Law; it explains conservation of angular momentum.
D) None of the above; it is not related to rotational motion.
31. Which of the following equations represents the relationship between linear velocity (v) and angular velocity (ω) for a rotating object with radius (r)?
A) v = ωr
B) v = r/ω
C) v = ω/r
D) v = r + ω
32. In a system of particles, what happens to the total angular momentum when the moment of inertia is increased while angular velocity remains constant?
A) Total angular momentum increases
B) Total angular momentum decreases
C) Total angular momentum remains constant
D) Total angular momentum becomes zero
33. When an ice skater with outstretched arms spins in a circle, and then pulls their arms close to their body while continuing to spin, what happens to their angular velocity?
A) Angular velocity increases
B) Angular velocity decreases
C) Angular velocity remains the same
D) Angular velocity reverses direction
34. What is the rotational analog of linear acceleration (a) in the context of angular motion?
A) Rotational velocity (ω)
B) Angular acceleration (α)
C) Torque (τ)
D) Angular momentum (L)
35. Which law of motion can be applied to relate the net external force to the change in linear momentum in rotational motion?
A) Newton's First Law
B) Newton's Second Law
C) Newton's Third Law
D) Law of Conservation of Linear Momentum
36. If a rigid body is in translational equilibrium, what can be concluded about its rotational motion?
A) It is in rotational equilibrium.
B) It has zero angular velocity.
C) It has zero angular acceleration.
D) It has infinite moment of inertia.
37. When an object is in uniform circular motion, what can be said about its angular velocity?
A) Angular velocity is constant.
B) Angular velocity changes direction.
C) Angular velocity is zero.
D) Angular velocity decreases over time.
38. What is the term for the rotational analog of force in linear motion, responsible for causing angular acceleration in rotational systems?
A) Torque (τ)
B) Angular velocity (ω)
C) Moment of inertia (I)
D) Angular momentum (L)
39. When a force is applied to the edge of a rotating door perpendicular to its plane, what physical quantity is responsible for causing the door to rotate?
A) Angular momentum
B) Torque
C) Linear velocity
D) Center of mass
40. In a closed system of particles with no external torques acting on it, what happens to the total angular momentum?
A) It decreases
B) It remains the same
C) It increases
D) It becomes zero
41. In a rotating system, what happens to the angular velocity when no net external torque acts on it?
A) Angular velocity remains constant
B) Angular velocity increases
C) Angular velocity decreases
D) Angular velocity reverses direction
42. Which of the following factors affects the moment of inertia of an object?
A) Angular velocity
B) Linear velocity
C) Shape and mass distribution
D) Torque
43. When a diver performs a twisting dive and rotates their body along the longitudinal axis, what type of motion is this?
A) Translational motion
B) Rotational motion
C) Combined translational and rotational motion
D) Projectile motion
44. What is the moment of inertia of a point mass m located at a distance r from an axis of rotation?
A) I = m/r^2
B) I = mr^2
C) I = m/r
D) I = r/m
45. In a closed system with no external torques, if one part of the system moves closer to the axis of rotation, what happens to the moment of inertia of that part?
A) Moment of inertia decreases
B) Moment of inertia increases
C) Moment of inertia remains the same
D) Moment of inertia becomes zero
46. Which physical quantity represents the resistance of an object to changes in its rotational motion and depends on the distribution of mass around its axis?
A) Angular velocity
B) Angular momentum
C) Moment of inertia
D) Torque
47. When a diver tucks into a somersault, why does their angular velocity increase?
A) Due to a decrease in moment of inertia
B) Due to a decrease in angular momentum
C) Due to a decrease in mass
D) Due to an increase in external torque
48. What is the condition for a system of particles to be in rotational equilibrium?
A) The net external torque is zero.
B) The total angular momentum is zero.
C) The sum of the external torques is zero.
D) The moment of inertia is infinite.
49. When a car accelerates and goes around a curve, what type of motion does its wheels experience?
A) Translational motion only
B) Rotational motion only
C) Combined translational and rotational motion
D) Oscillatory motion
50. What is the rotational analog of linear velocity (v) in the context of angular motion?
A) Angular velocity (ω)
B) Angular acceleration (α)
C) Torque (τ)
D) Moment of inertia (I)
51. When a force is applied tangentially to a rotating object in the direction of its motion, what effect does it have on the object's angular velocity?
A) Angular velocity increases
B) Angular velocity decreases
C) Angular velocity remains the same
D) Angular velocity becomes zero
52. In a rotating system, if the moment of inertia is halved while angular velocity remains constant, what happens to the system's rotational kinetic energy?
A) Rotational kinetic energy increases
B) Rotational kinetic energy decreases
C) Rotational kinetic energy remains the same
D) Rotational kinetic energy becomes zero
53. What is the rotational analog of linear momentum (p) in the context of angular motion?
A) Angular velocity (ω)
B) Angular acceleration (α)
C) Angular momentum (L)
D) Moment of inertia (I)
54. When a rigid object rotates about a fixed axis, what is the relationship between the linear velocity of a point on the object and its distance from the axis of rotation?
A) Linear velocity is directly proportional to distance from the axis.
B) Linear velocity is inversely proportional to distance from the axis.
C) Linear velocity is unrelated to distance from the axis.
D) Linear velocity is equal to distance from the axis.
55. What is the condition for a system of particles to be in translational equilibrium?
A) The net external force is zero.
B) The total angular momentum is zero.
C) The sum of the external forces is zero.
D) The moment of inertia is infinite.
56. When an object is in equilibrium and subject to a net external torque, what happens to its angular acceleration?
A) Angular acceleration increases
B) Angular acceleration decreases
C) Angular acceleration remains the same
D) Angular acceleration becomes zero
57. What is the rotational analog of work (W) in linear motion, representing the energy transfer due to the application of a torque?
A) Angular velocity (ω)
B) Angular acceleration (α)
C) Torque (τ)
D) Angular momentum (L)
58. In a rotating system, if the angular velocity is doubled while the moment of inertia remains constant, what happens to the system's rotational kinetic energy?
A) Rotational kinetic energy increases by a factor of 2
B) Rotational kinetic energy increases by a factor of 4
C) Rotational kinetic energy decreases by a factor of 2
D) Rotational kinetic energy remains the same
59. What is the term for the point in a rotating system where the net external force causes no change in the linear velocity of a point on the object?
A) Axis of rotation
B) Center of mass
C) Equilibrium point
D) Torque point
60. When a rotating wheel experiences a net external torque in the direction opposite to its rotation, what happens to its angular acceleration?
A) Angular acceleration increases
B) Angular acceleration decreases
C) Angular acceleration remains the same
D) Angular acceleration reverses direction
61. In a rotating system, if the net external torque is directed opposite to the direction of rotation, what will happen to the angular velocity?
A) Angular velocity increases
B) Angular velocity decreases
C) Angular velocity remains constant
D) Angular velocity reverses direction
62. When a diver executes a twisting dive, what physical quantity remains constant throughout the dive, assuming no external torques are acting?
A) Angular velocity
B) Angular momentum
C) Moment of inertia
D) Torque
63. When a force is applied to a rotating object perpendicular to its plane, what physical quantity is responsible for causing the object to rotate?
A) Angular velocity
B) Angular acceleration
C) Torque
D) Linear velocity
64. What is the relationship between the angular velocity (ω) and the time (t) taken for an object to complete one full rotation (period T) in a uniform circular motion?
A) ω = T/t
B) ω = 2π/T
C) ω = 2πt/T
D) ω = T/2πt
65. In a system of particles, what effect does an increase in the net external torque have on the system's angular momentum?
A) Angular momentum increases
B) Angular momentum decreases
C) Angular momentum remains constant
D) Angular momentum reverses direction
66. When a diver tucks into a somersault, what happens to their moment of inertia?
A) Moment of inertia decreases
B) Moment of inertia increases
C) Moment of inertia remains the same
D) Moment of inertia reverses direction
67. What is the condition for a system of particles to be in translational equilibrium?
A) The net external force is zero.
B) The total angular momentum is zero.
C) The sum of the external forces is zero.
D) The moment of inertia is zero.
68. When a rigid body is in translational motion, what can be said about its angular velocity?
A) Angular velocity is constant.
B) Angular velocity changes direction.
C) Angular velocity is zero.
D) Angular velocity decreases over time.
69. What is the term for the rotational analog of kinetic friction in linear motion, which opposes the relative motion between two surfaces in contact?
A) Angular velocity
B) Angular acceleration
C) Torque
D) Angular momentum
70. If a system of particles is in translational equilibrium, what can be concluded about its rotational motion?
A) It is in rotational equilibrium.
B) It has zero angular velocity.
C) It has zero angular acceleration.
D) It has infinite moment of inertia.
In conclusion, mastering the System of Particles and Rotational Motion is essential for success in the HTET 2023. These MCQs, accompanied by expert tips, can serve as a powerful tool in your exam preparation. Remember to practice regularly, analyze your mistakes, and strengthen your conceptual understanding. With dedication and a strategic approach, you can confidently tackle this section and excel in the upcoming HTET. Best of luck with your preparations and the exam ahead!







No comments:
Post a Comment